Mathematics and statistics



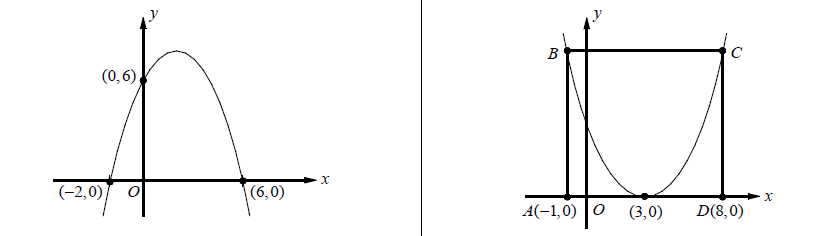
Quadratic function
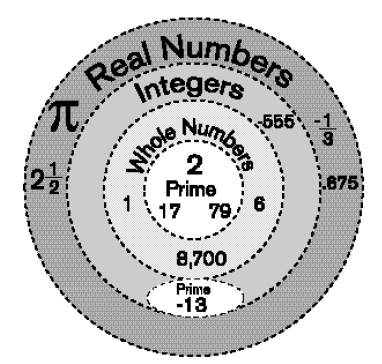
In Algebra, a quadratic function is a polynomial function in which the highest-degree term is of the second degree.
The graph of a quadratic function is a curve called a parabola. Parabolas may open upward or downward and vary in "width" or "steepness", but they all have the same basic "U" shape. All parabolas are symmetric with respect to a line called the axis of symmetry. A parabola intersects its axis of symmetry at a point called the vertex of the parabola.
A univariate quadratic function can be expressed in three formats: standard form, factored form and vertex form. Standard form is f(x)=ax^2+bx+c, where a,b and c are coefficients and a cannot be zero. Factored form is f(x)=a(x-r1)(x-r2) where r1and r2 are the roots of the quadratic function and the solutions of the corresponding quadratic equation. Vertex form is f(x)=a(x-h)^2+k, where h and k are the x and y coordinates of the vertex, respectively. The coefficient a has the same value in all three forms.
If coefficient a > 0, the parabola opens upwards. If a < 0, the parabola opens downwards. The coefficient a controls the degree of curvature of the graph, a larger magnitude of a gives the graph a more closed (sharply curved) appearance. The coefficients b and a together control the location of the vertex (T(h,k)), where h=-b/a and k=(-b^2+4ac)/4a. The coefficient c is the height of the parabola where it intercepts the y-axis.



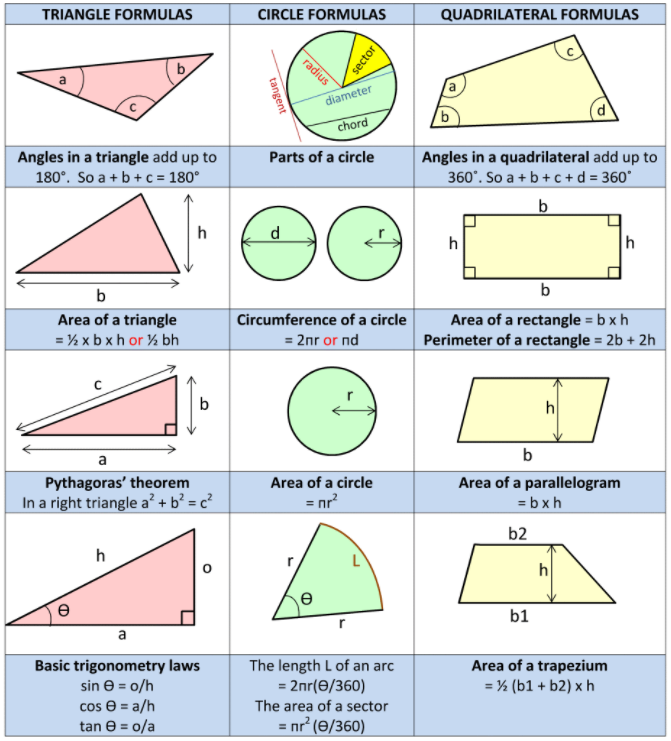
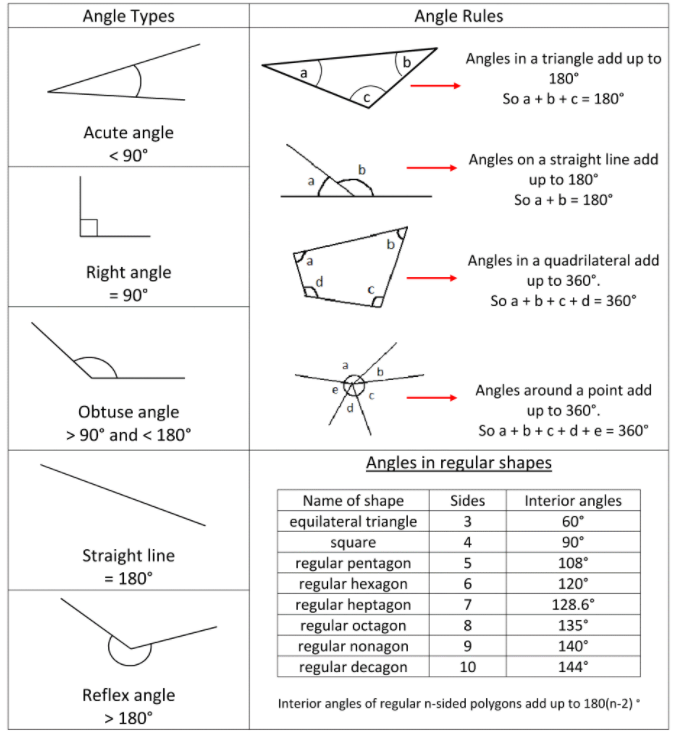



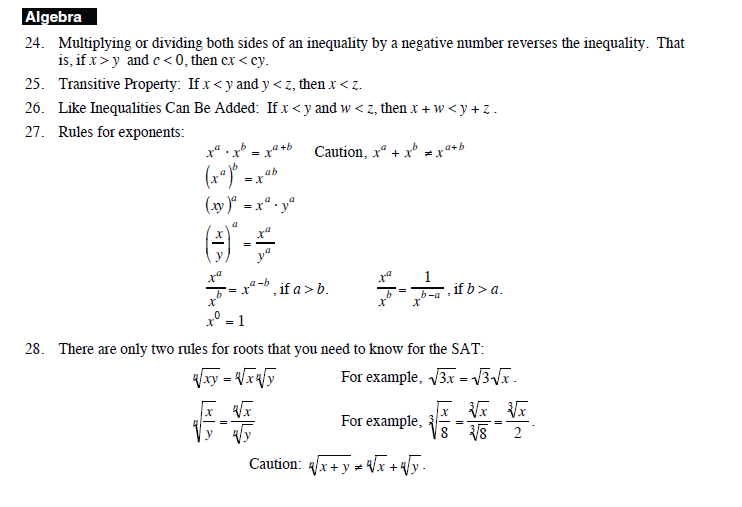

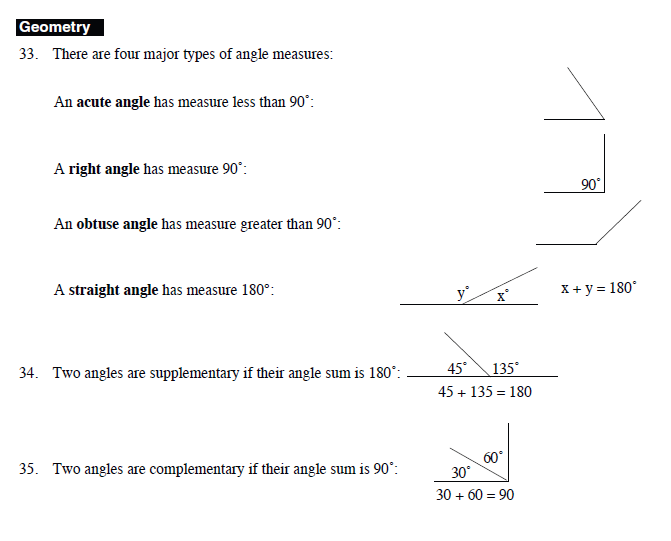








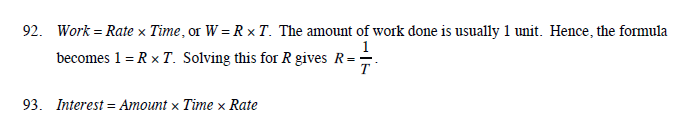
MATERIJALI I LITERATURA
Arithmetics Aritmethics.pdf
Algebra Algebra.pdf
Geometry Geometry.pdf
Word problems Word Problems.pdf
Formulae:
Resources:SAT_Math_Essentials.pdf
Tests: SAT Math test.pdf
Solutions: SAT-Math-Answers and Solutions .pdf
Greek alphabet: greek_alphabet.mp3
Math dictionary:
Additional materials: 501MathWordProblems.pdf
Kaplan math: